| RXDDRUG | RXDDAYS | LBXIN | LBXGH | LBDLDL | LBXTR | LBDHDD | LBXTC | URXUMA | BPXSY1 | BPXDI1 | BMXBMI | BMXWAIST | RIDAGEYR | RIAGENDR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| INSULIN ASPART | 365 | 5.83 | 8.9 | 56 | 51 | 60 | 126 | 11.9 | 140 | 90 | 28.9 | 109.2 | 72 | Male |
| GLIPIZIDE | 4745 | 5.91 | 6.0 | 71 | 108 | 47 | 140 | 29.2 | 138 | 56 | 24.8 | 98.0 | 63 | Female |
{BayesCVI}
A Bayesian cluster validity index with medical applications
King Mongkut’s University of Technology Thonburi
Objective
Learn prescribed drugs patterns through clustering
Why it matters
What we will cover today
- Background
- Motivation
- A Bayesian cluster validity index
- Introduction to the
BayesCVIpackage - Conclusion
Public health issue
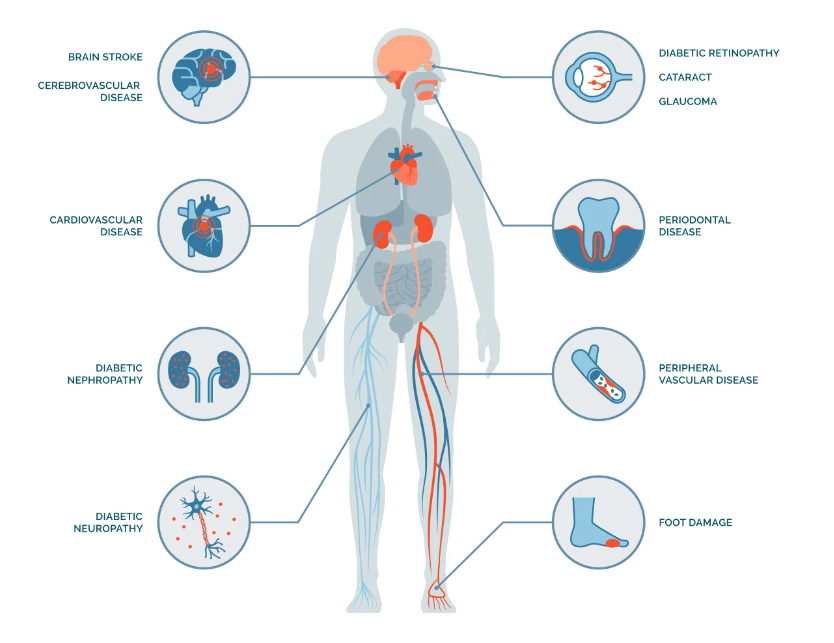
Diabetes is a chronic, metabolic disease characterized by elevated levels of blood glucose (or blood sugar), which leads over time to serious damage to the heart, blood vessels, eyes, kidneys and nerves.
Diabetes
Diabetes is a global health crisis that has seen a dramatic rise in recent years. According to World Health Organization in 2021, it ranked among the top 10 causes of death worldwide, with a staggering 95% increase since 2000.
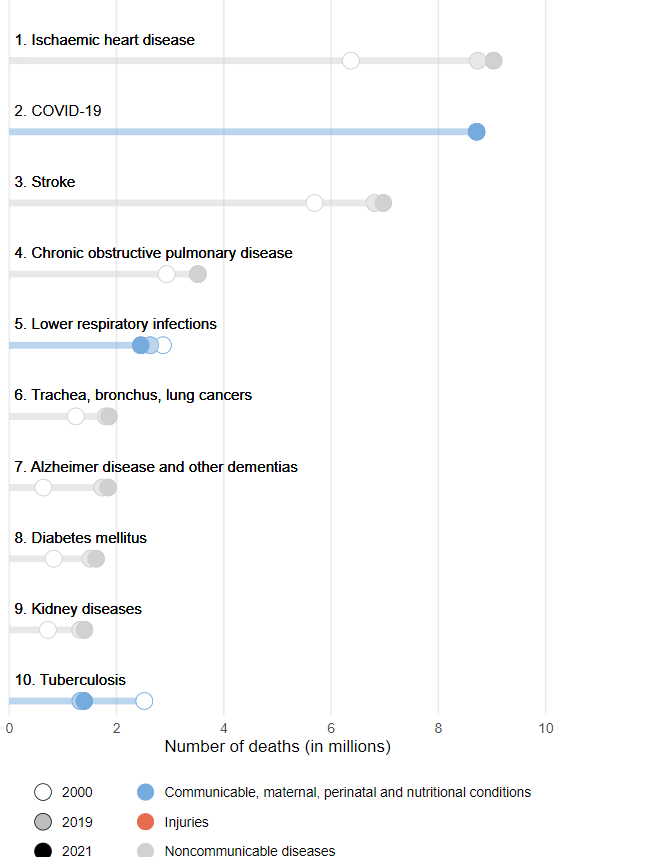
Data overview
National Health and Nutrition Examination Survey (NHANES) datasets from 2013-2014 Source: National Health and Nutrition Examination Survey
Information: 207 diabetes patients, including 15 variables.
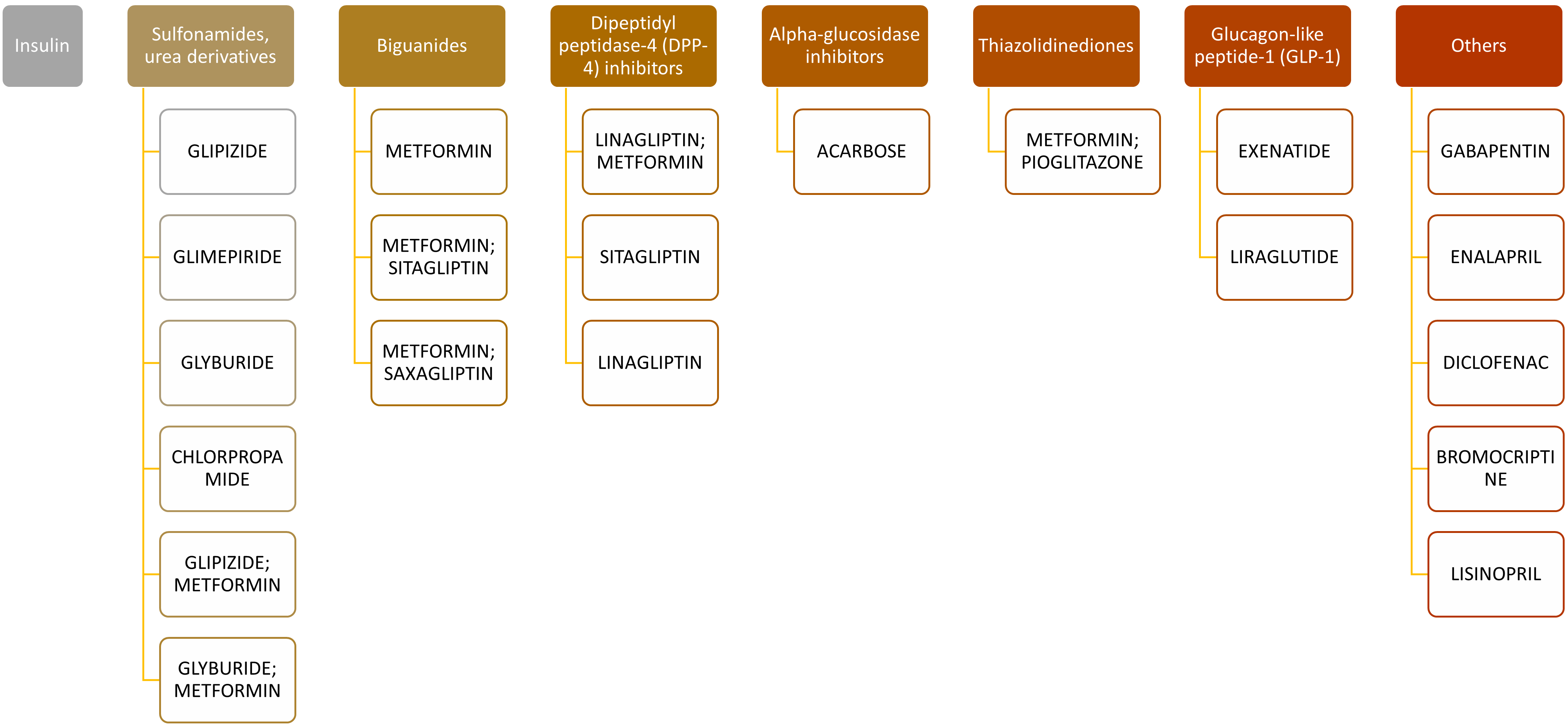
Medications
| Variable | Description |
|---|---|
| RXDDRUG | Generic drug name |
| RXDDAYS | For how long have you been using or taking PRODUCT NAME? |
Laboratory results
| Variable | Description |
|---|---|
| LBXIN | Insulin (uU/mL) |
| LBXGH | Glycohemoglobin (%) |
| LBXTR | Triglyceride (mg/dL) |
| LBDLDL | LDL-cholesterol (mg/dL) |
| LBDHDD | Direct HDL-Cholesterol (mg/dL) |
| LBXTC | Total Cholesterol (mg/dL) |
| URXUMA | Albumin, urine (ug/mL) |
Medical examinations
| Variable | Description |
|---|---|
| BPXSY1 | Systolic: Blood pressure (first reading) (mm Hg) |
| BPXDI1 | Diastolic: Blood pressure (first reading) (mm Hg) |
| BMXBMI | Body Mass Index (kg/m²) |
| BMXWAIST | Waist Circumference (cm) |
Demographics
| Variable | Description |
|---|---|
| RIDAGEYR | Age in years of the participant at the time of screening |
| RIAGENDR | Gender of the participant |
Classes of diabetic drugs in this data
Background
Cluster analysis (CA) is an unsupervised learning tool in machine learning that is widely used in various areas.

The aim is to identify natural groupings within a dataset that are not initially apparent and without prior knowledge of the groups.
Ref: Figure
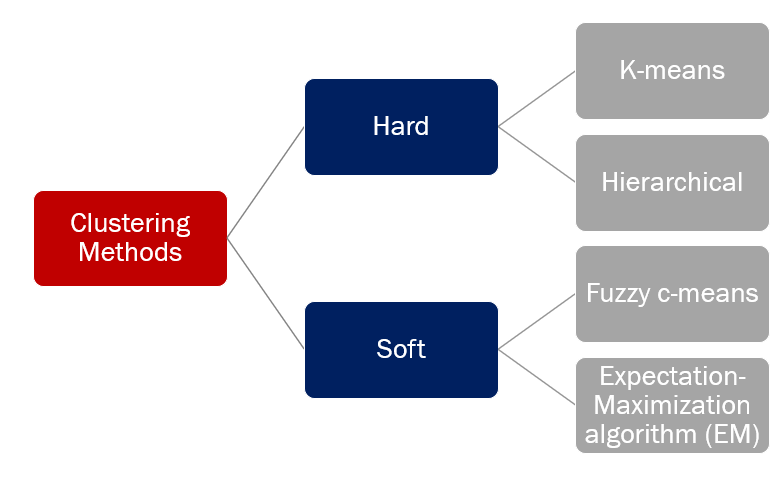
Clustering algorithms
Determining the number of clusters
Elbow method
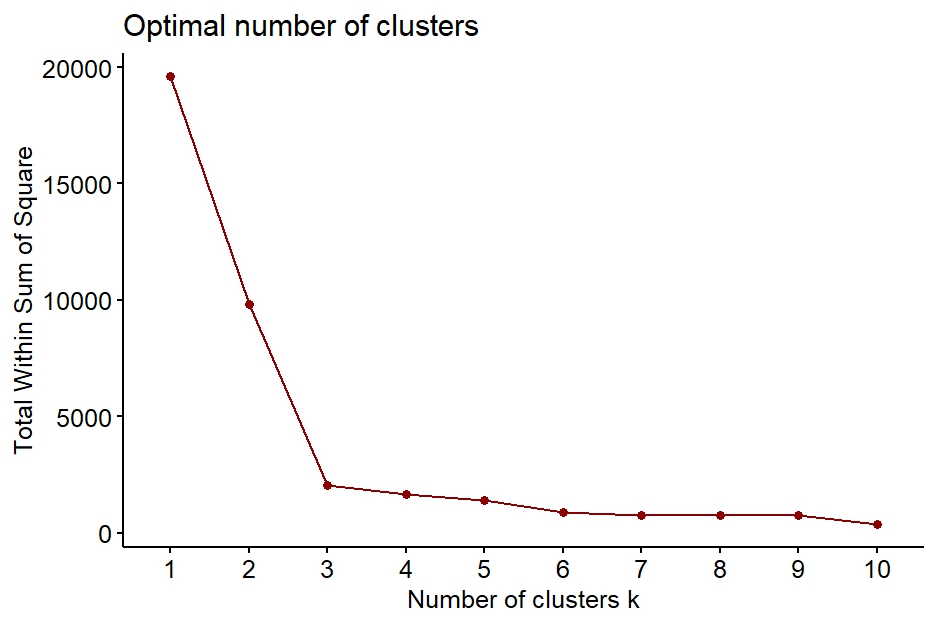
Determining the number of clusters
Cluster Validity index (CVI)
Hard:
- Dunn’s Index 1973
- Calinski-Harabasz 1974
- Davies-Bouldin’s index 1979
- Point biserial correlation 1980
- Silhouette coefficient (Rousseeuw [1987], Sarle [1991])
- Generalized Dunn index 1998
- PBM index 2004
- Chou-Su-Lai index 2004
- Davies-Bouldin index 2005
- STR index 2017
- Wiroonsri index 2024
Soft:
- Xie–Beni (XB) index 1991
- Pakhira–Bandyopadhyay–Maulik (PBM) index 2004
- TANG index 2005
- Wu–Li (WL) index 2015
- Generalized C index 2016
- KWON2 index 2021
- Wiroonsri and Preedasawakul (WP) index
Applying CVI
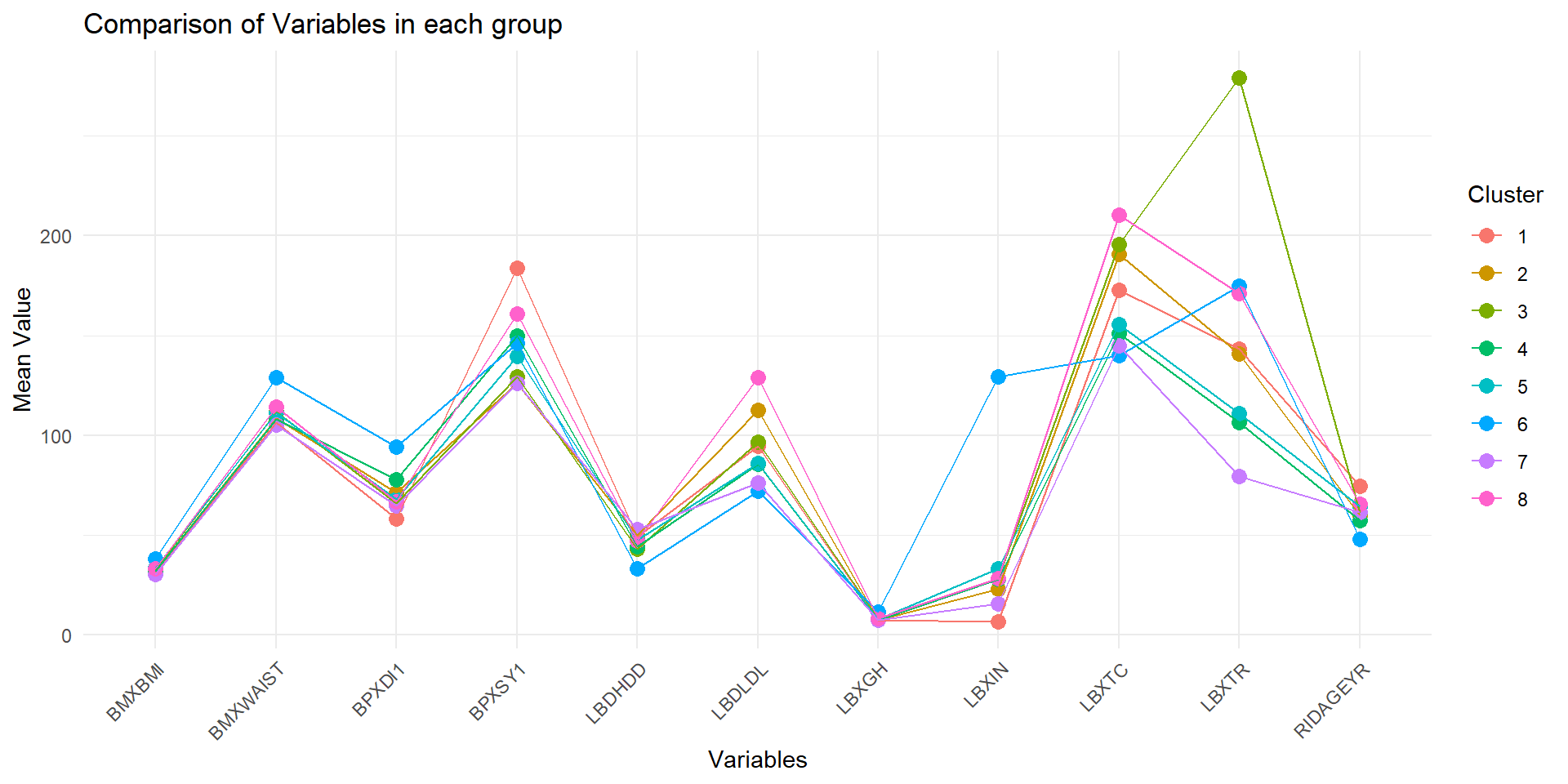
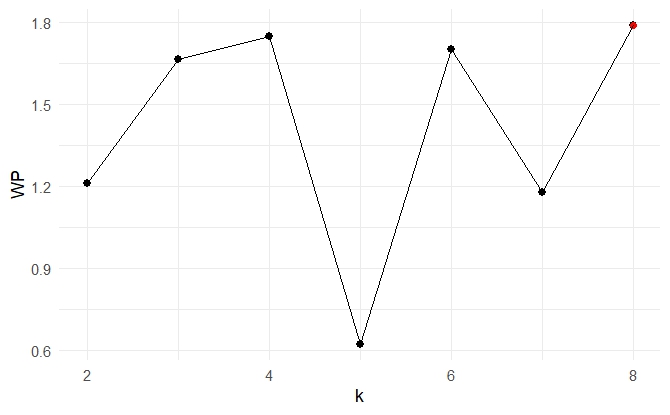
Cluster the data into 8 groups
| cc | RXDDAYS | LBXIN | LBXGH | LBDLDL | LBXTR | LBDHDD | LBXTC | URXUMA | BPXSY1 | BPXDI1 | BMXBMI | BMXWAIST | RIDAGEYR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4628.000 | 6.753333 | 7.466667 | 94.66667 | 143.33333 | 49.33333 | 172.6667 | 3566.66667 | 184.0000 | 58.00000 | 31.63333 | 106.4667 | 74.33333 |
| 2 | 1562.987 | 23.088125 | 7.451250 | 112.56250 | 140.73750 | 50.15000 | 190.9000 | 18.96500 | 126.1000 | 71.17500 | 31.89125 | 108.4963 | 59.82500 |
| 3 | 1748.379 | 28.413448 | 7.827586 | 96.62069 | 279.17241 | 43.10345 | 195.5172 | 49.73448 | 129.5172 | 65.79310 | 32.81724 | 111.9759 | 60.89655 |
| 4 | 3066.000 | 27.914000 | 7.320000 | 85.40000 | 106.60000 | 44.40000 | 151.2000 | 1020.00000 | 150.0000 | 78.00000 | 31.94000 | 108.1600 | 57.20000 |
| 5 | 2673.059 | 33.377647 | 7.858823 | 85.94118 | 111.05882 | 47.52941 | 155.6471 | 298.79412 | 139.7647 | 68.00000 | 33.63529 | 111.5059 | 64.29412 |
| 6 | 14.000 | 129.340000 | 11.600000 | 72.00000 | 175.00000 | 33.00000 | 140.0000 | 7400.00000 | 146.0000 | 94.00000 | 38.20000 | 128.8000 | 48.00000 |
| 7 | 1877.149 | 15.616418 | 7.246269 | 76.35821 | 79.41791 | 52.70149 | 144.9254 | 20.36866 | 126.0299 | 64.71642 | 30.14328 | 105.2075 | 61.53731 |
| 8 | 3139.000 | 28.394000 | 8.280000 | 128.80000 | 171.00000 | 47.20000 | 210.4000 | 1924.80000 | 160.8000 | 66.80000 | 33.38000 | 114.2800 | 65.40000 |
Motivation
What if the optimal number is not what we are looking for?

Brain MRI: tumor detection
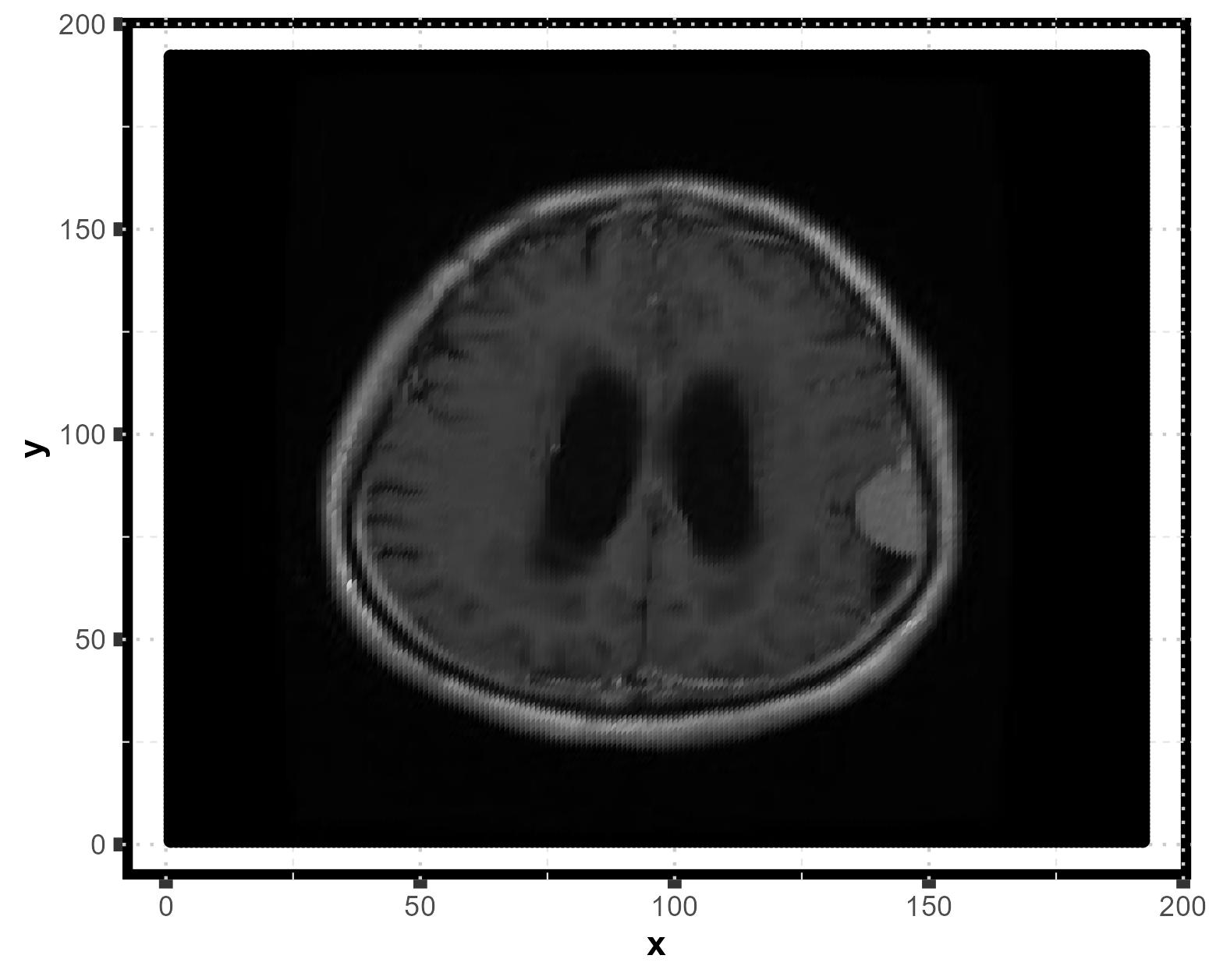
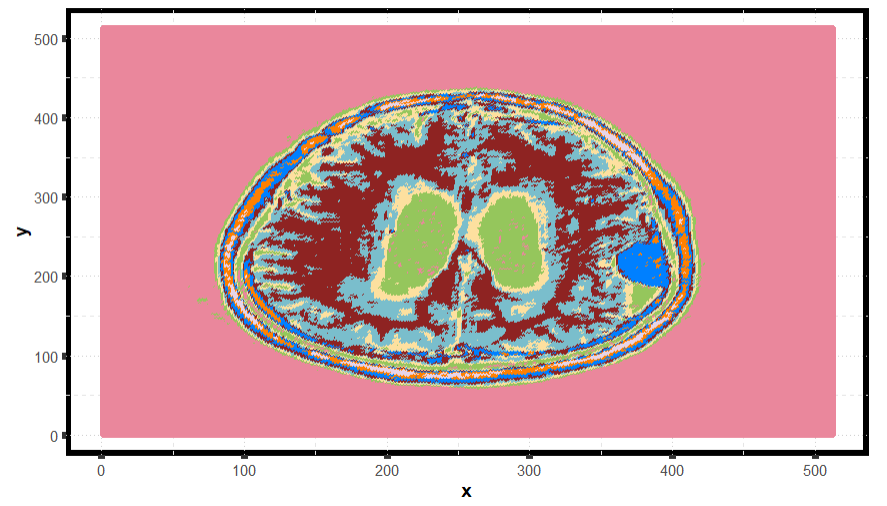
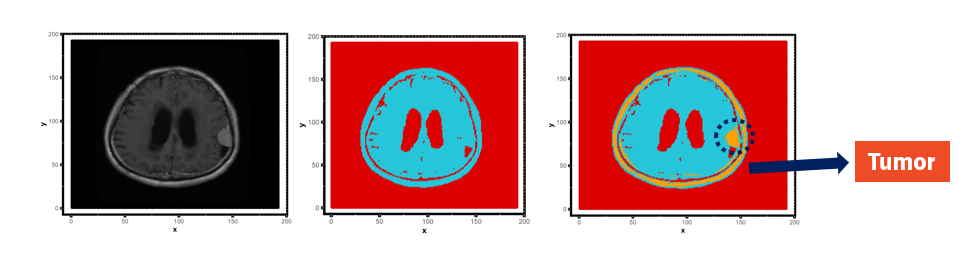
Ref: https://www.kaggle.com/datasets/masoudnickparvar/brain-tumor-mri-dataset
Bayesian framework and cluster validity index
Idea
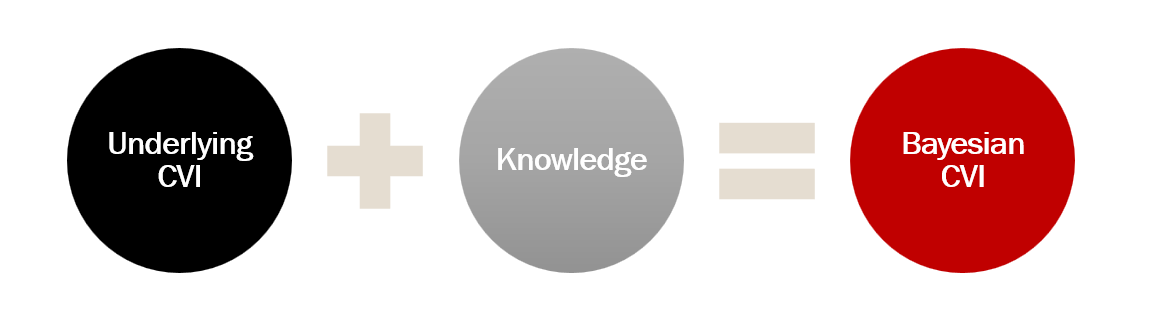
Bayesian framework and cluster validity index
To be more precise…
Notations
- \({\bf x} = (x_1,x_2,\ldots,x_n)\) denotes a dataset of size \(n \in \mathbb{N}\).
- \(K \in \mathbb{N}\) is the maximum number of clusters to be considered
- \({\bf p} = (p_2,p_3,\ldots,p_K)\), where \(p_k\), \(k=2,3,\ldots,K\) represents the probability that the actual number of groups is \(k\).
Background of BCVI
Assume that
\[ f({\bf x}|{\bf p}) = C({\bf p}) \prod_{k=2}^Kp_k^{nr_k(x)} \qquad(1)\]
represents the conditional probability density function of the dataset given \({\bf p}\), where \(C({\bf p})\) is the normalizing constant for the probability density function.
Background of BCVI
Let \(r_k(\bf x)\) be a ratio adjusted from a CVI defined as
\[ r_k(\bf x) = \begin{cases} \dfrac{GI(k)-\min_j GI(j)}{\sum_{i=2}^K (GI(i)-\min_j GI(j))} \text{ for Condition A, } \\ \dfrac{\max_j GI(j)- GI(k)}{\sum_{i=2}^K (\max_j GI(j) - GI(i))} \text{ for Condition B, } \\ \end{cases} \qquad(2)\]
where GI represents an arbitrary CVI.
Condition A: The largest value of the GI indicates the optimal number of clusters.
Condition B: The smallest value of the GI indicates the optimal number of clusters.
It is clear that \(0\le r_k(\bf x) \le 1\).
Dirichlet prior
Here, we assume that \({\bf p}\) follows a Dirichlet prior distribution with parameters \({\bf \alpha} = (\alpha_2,\ldots,\alpha_K)\) with the probability density function
\[ \pi({\bf p}) = \frac{1}{B({\bf \alpha})} \prod_{k=2}^K p_k^{\alpha_k-1}. \]
Reference: Dirichlet distribution
Dirichlet posterior
Let \(K \in \mathbb{N}\) and \({\bf r(x)} = (r_2({\bf x}),\ldots,r_K({\bf x}))\), where \(r_k({\bf x})\) is defined as in (1). Assuming that \({\bf x}\) follows the distribution described in (2), the posterior distribution of \({\bf p}\) has the probability density function:
\[
\pi({\bf p}|{\bf x}) = \frac{f({\bf x , p})}{m({\bf x})} = \frac{1}{B({\bf \alpha} + n{\bf r(x)})} \prod_{k=2}^K p_k^{\alpha_k+nr_k({\bf x})-1}.
\]
In particular, it follows a Dirichlet distribution with parameters \({\bf \alpha}+ n{\bf r(x)}\).
Definition of BCVI
For \(k = 2,3,\ldots,K\), the BCVI is then defined as
\[ \texttt{BCVI}(k) = E[p_k|{\bf x}] = \frac{\alpha_k + nr_k({\bf x})}{\alpha_0+n} \]
where \(\alpha_0 = \sum_{k=2}^K \alpha_k\).
{BayesCVI}
BayesCVI
The BayesCVI package is an R package that allows users to apply the Bayesian Cluster Validity Index (BCVI) to their clustering results.
- The package is compatible with K-means, fuzzy C means, EM clustering, and hierarchical clustering (single, average, and complete linkage).
- BCVI is compatible with any existing underlying CVIs
Arguments and parameter \(\alpha\)
Wiroonsri index (Hard)
The default alpha value corresponds to the case where \(\alpha_k=1\) for all k. This is used when users want the results to rely only on underlying CVIs.
Alpha
How to apply
# Determine alpha based on our knowledge
# Consider k from 2 to 10
aalpha = c(25,25,25,25,25,5,5,5,5)
set.seed(50)
B.WI = B_Wvalid(x = scale(clustdata), kmax = 10, method = "kmeans",
corr = "pearson",nstart = 10, sampling = 1, NCstart = TRUE,
alpha = aalpha, mult.alpha = 1/2)
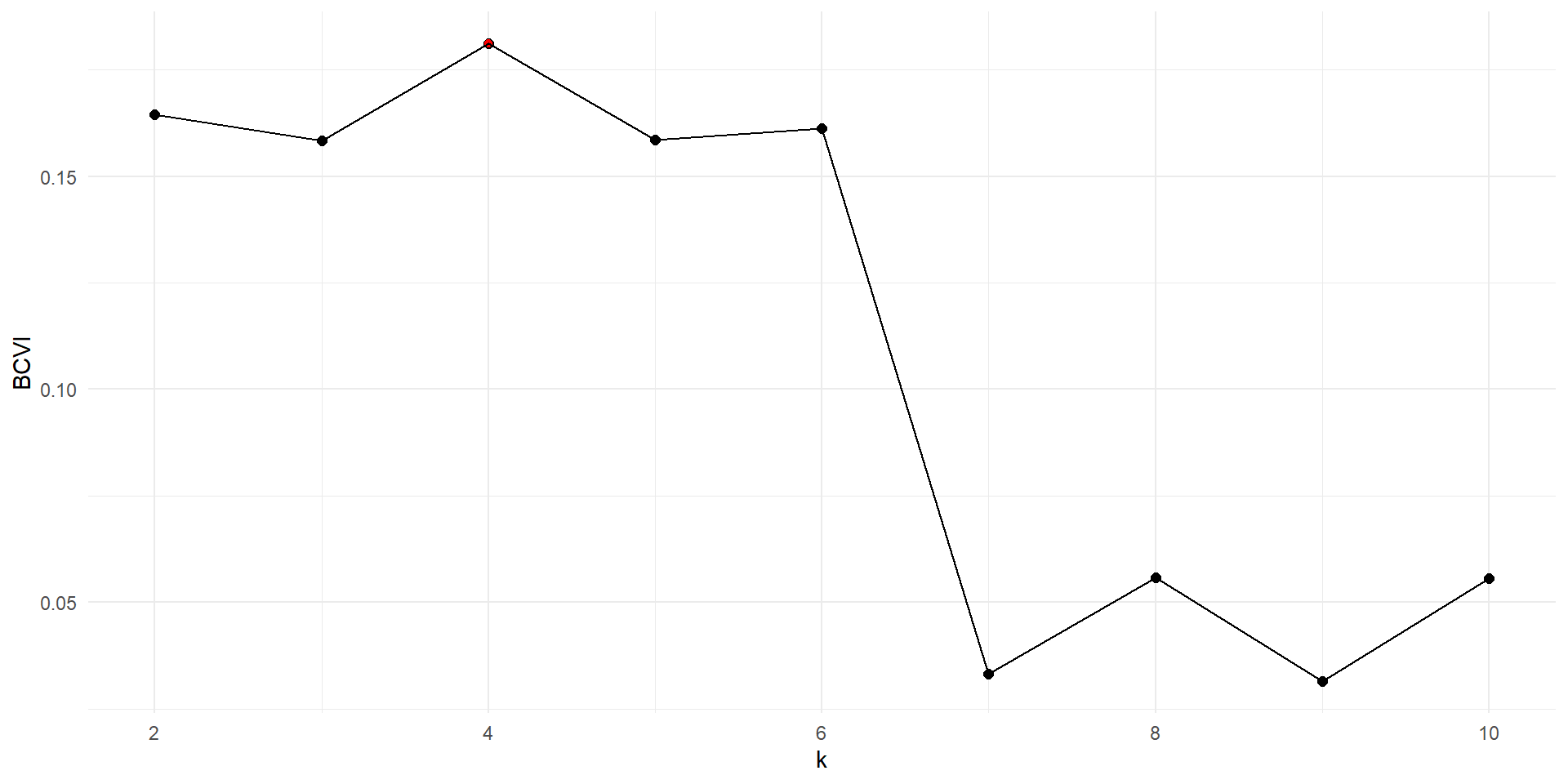
B.WI$BCVI
k BCVI
1 2 0.16458037
2 3 0.15846049
3 4 0.18115842
4 5 0.15863418
5 6 0.16133557
6 7 0.03308408
7 8 0.05575108
8 9 0.03137009
9 10 0.05562574
$VAR
k Var
1 2 5.993133e-05
2 3 5.812551e-05
3 4 6.465910e-05
4 5 5.817721e-05
5 6 5.897794e-05
6 7 1.394373e-05
7 8 2.294621e-05
8 9 1.324478e-05
9 10 2.289766e-05
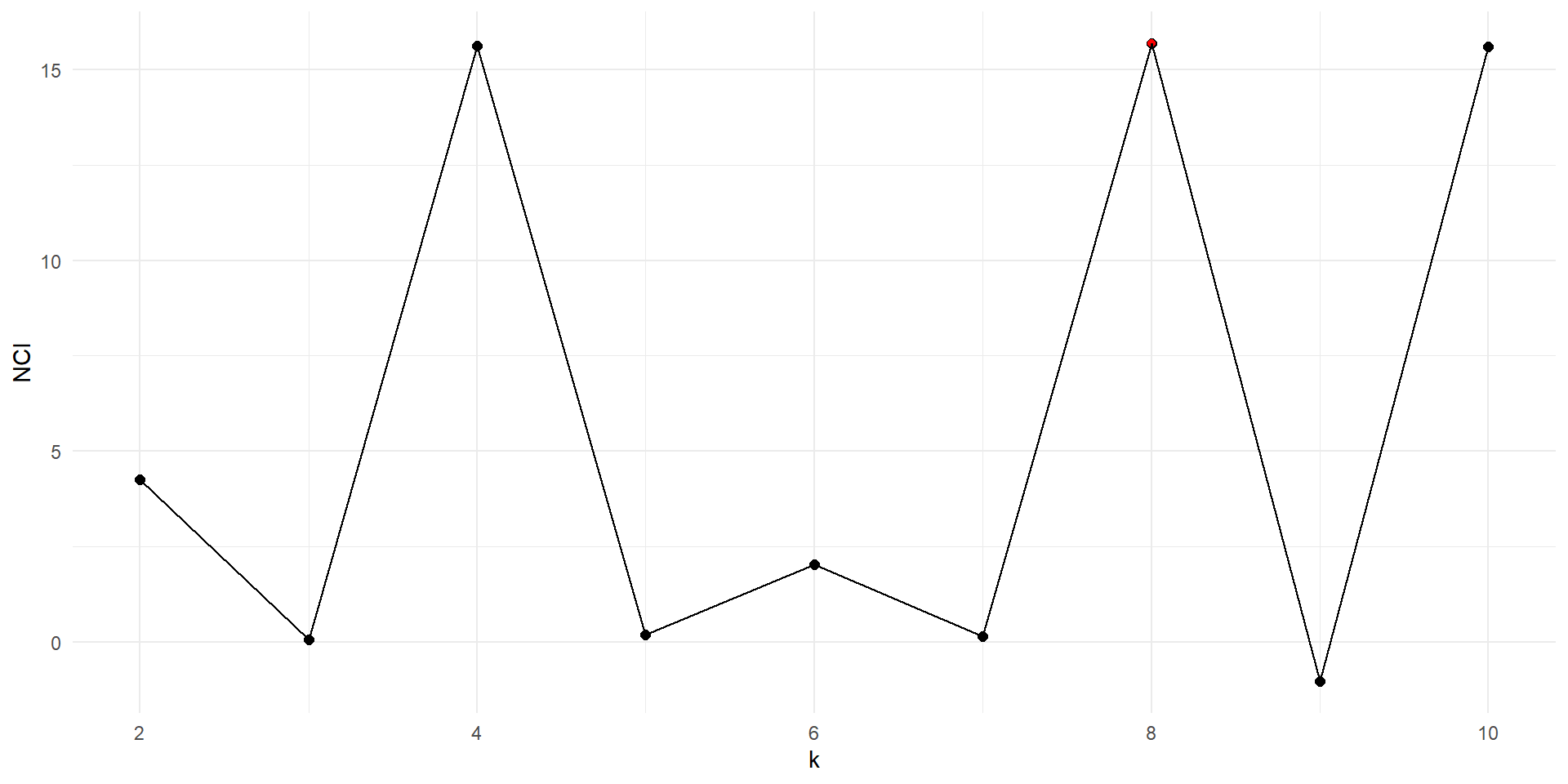
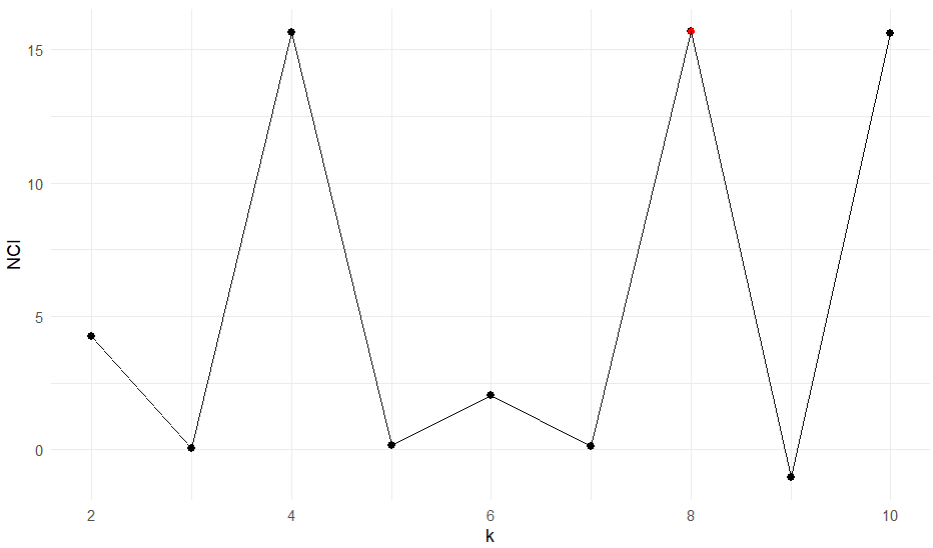
$Index
k NCI
1 2 4.26091013
2 3 0.06102601
3 4 15.63792156
4 5 0.18022009
5 6 2.03410523
6 7 0.13235949
7 8 15.68803415
8 9 -1.04389746
9 10 15.60201492Visualize the result
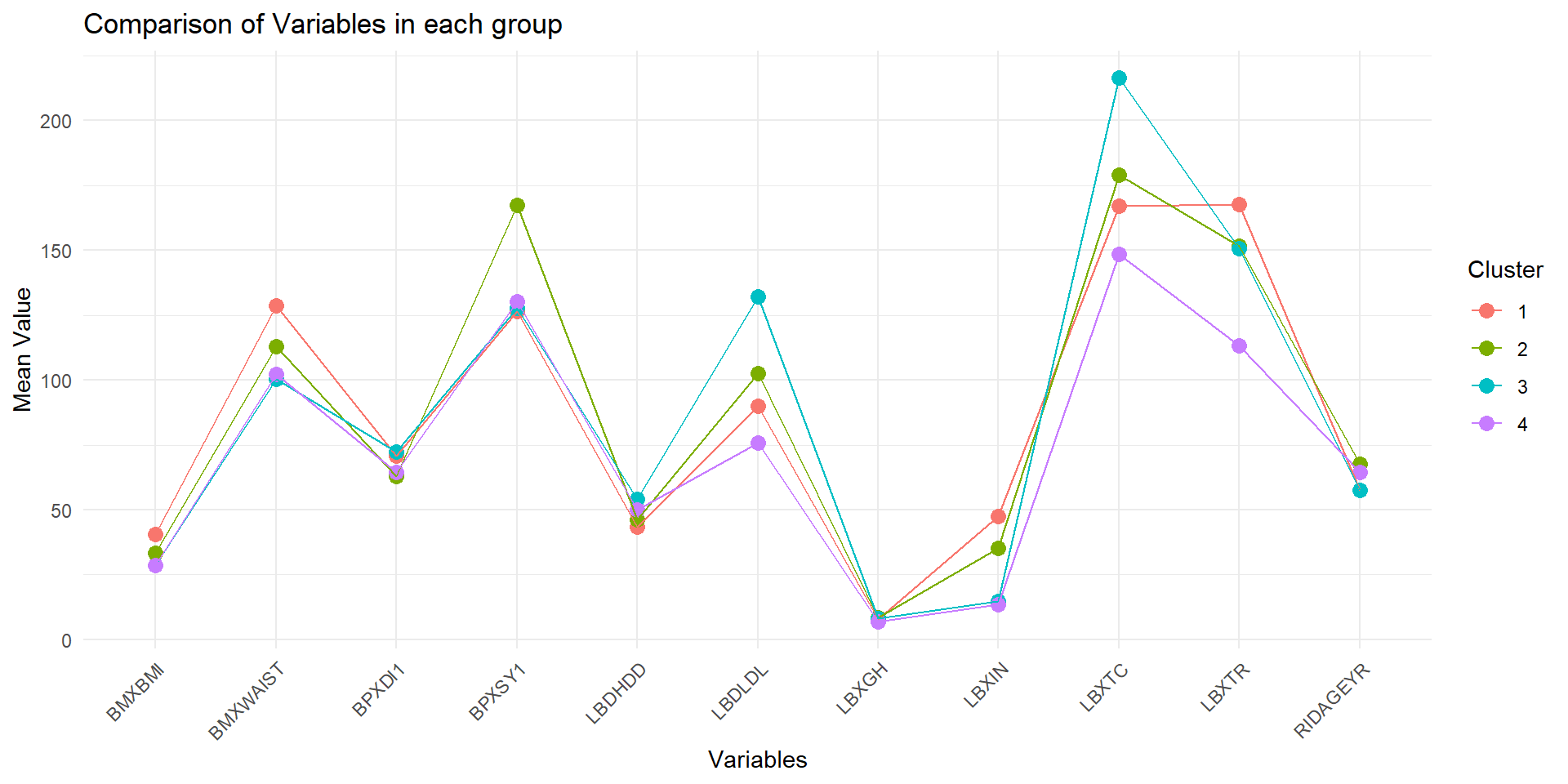
Cluster the data into 4 groups
| cc | RXDDAYS | LBXIN | LBXGH | LBDLDL | LBXTR | LBDHDD | LBXTC | URXUMA | BPXSY1 | BPXDI1 | BMXBMI | BMXWAIST | RIDAGEYR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1392.918 | 47.38816 | 7.669388 | 90.00000 | 167.8571 | 43.48980 | 167.0612 | 99.62857 | 126.4082 | 70.61224 | 40.59184 | 128.7592 | 57.67347 |
| 2 | 3516.625 | 35.09375 | 8.387500 | 102.50000 | 151.5000 | 46.25000 | 179.1250 | 3250.50000 | 167.5000 | 62.75000 | 33.40000 | 113.0875 | 67.75000 |
| 3 | 1598.439 | 14.88439 | 8.098246 | 132.15789 | 150.5789 | 54.14035 | 216.4912 | 73.45965 | 127.6491 | 72.24561 | 28.66140 | 100.3474 | 57.43860 |
| 4 | 2197.624 | 13.59914 | 6.986021 | 75.78495 | 113.3011 | 50.03226 | 148.4409 | 76.93226 | 130.1720 | 64.58065 | 28.64731 | 102.1312 | 64.62366 |
Characteristic comparison
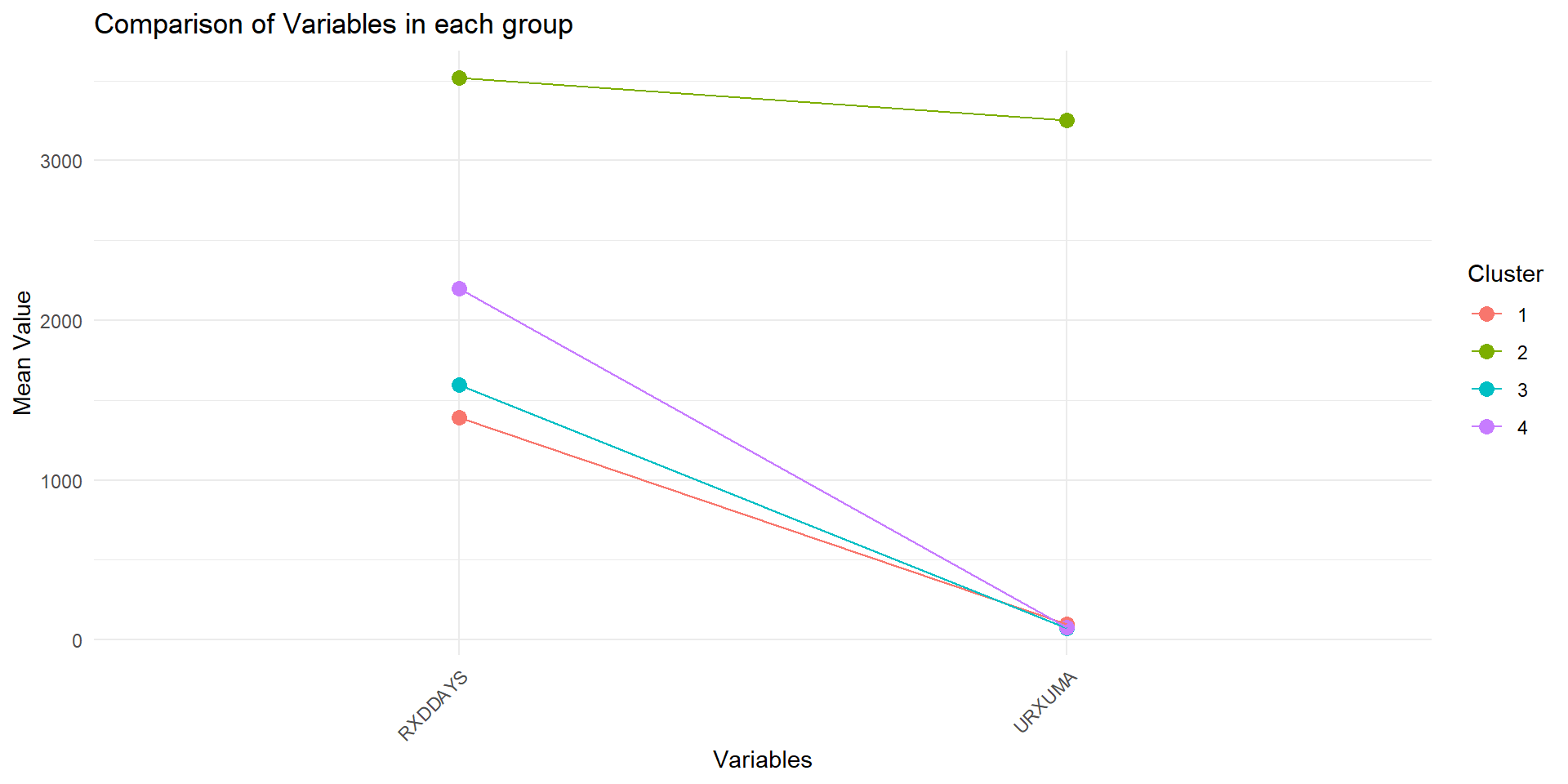
Characteristic comparison
| Characteristic | Group 1 | Group 2 | Group 3 | Group 4 |
|---|---|---|---|---|
| Number of Patients | 49 | 8 | 57 | 93 |
| Insulin Levels | Highest | Slightly elevated | Low | Lowest |
| Glucose Levels | Slightly elevated | Slightly higher | Moderate | Moderate |
| BMI | Severe obesity, highest BMI | Overweight, not as high as Group 1 | Normal BMI | Normal BMI |
| Waist Circumference | Largest, abdominal obesity | Elevated | Smaller than Groups 1 and 2 | Smaller than Groups 1 and 2 |
| Albumin Levels | Slightly high | Extremely elevated | Moderate | Moderate |
| Age | 57 | 68 | 57 | 65 |
Distribution of drugs used in each group
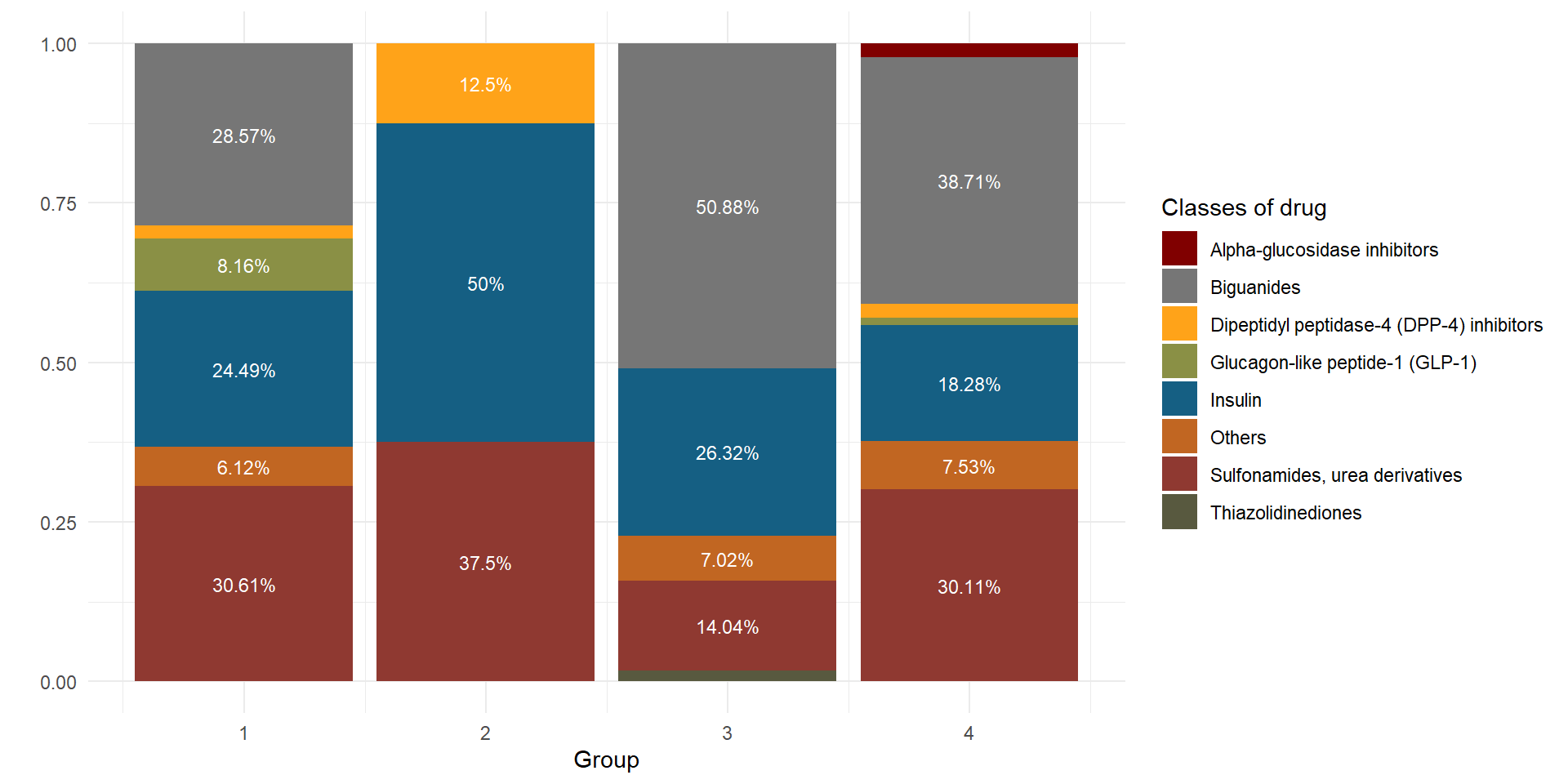
Potential benefit
It provides a valuable database for healthcare professionals, supporting informed decision-making, developing treatment strategies, and enhancing drug efficacy.
Highlighted Features for BCVI
Novel and unique concept: BCVI allows users to specify their desired range for the final number of clusters.
Flexibility: BCVI allows users to flexibly set parameters according to their needs and select any clustering algorithms and underlying CVIs of their choice.
Drawbacks
It relies on the quality of underlying indices.
It is only effective when underlying indices are present, providing meaningful options for ranking local peaks for the final number of clusters.
Explore more
Installation
Function
References
Acknowledgement
Nathakhun would like to also thank National Research Council of Thailand (NRCT), Grant number: N42A660991 (2023) for the project financial support.
Q&A
R/Pharma APAC 2024